Emergence is the new hot topic in AI Research. When I first heard of it in a Sanjeev Arora talk, the word felt heavy, profound, mysterious. I thought of genesis; it evoked in me visions of consciousness emerging out of ether. It took me back to the “More is Different” essay by PW Anderson. In short, it stirred…feelings.
Emergence is an observation that, as you scale up an AI model, for instance in the number of parameters, the model suddenly acquires an ability to solve new problems; an emergent ability is one that is not present in smaller models but exists in larger models. Many language models have been shown to demonstrate emergence across many tasks (adding numbers, unscrambling words etc.), even raising existential concerns that, perhaps, AI models will one day develop some ability we don’t quite fathom yet. Two key features of the emergence, as it has been noted, are unpredictability and suddenness. As you make the models bigger, there is some kind of transition between the model performing poorly on task X and it performing very well on the same task. Unpredictability means that for any given task (say writing Python code), it is not possible to anticipate at what parameter size such a sudden jump in performance appears.
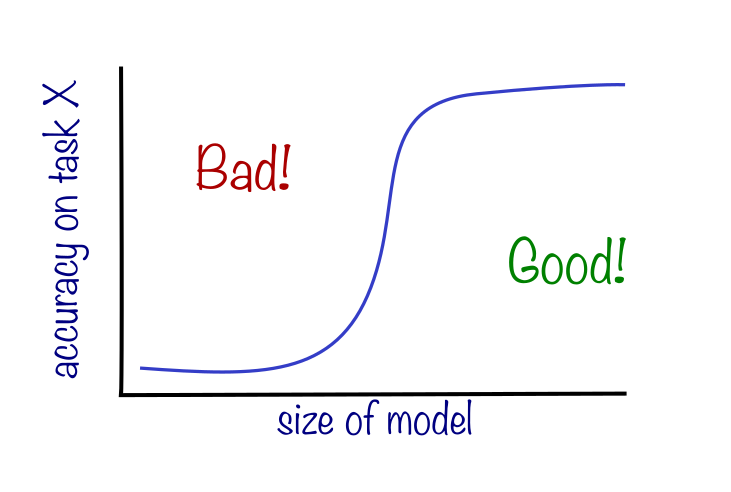
A provocative paper, which recently was awarded the best-paper award at NeurIPS 2023, has brought new attention to emergence. The paper argues that the emergent behavior researchers have hitherto observed is simply a delusion due to researchers looking at the wrong and complex metrics, and that if you only looked at simple (or as the paper argues: correct) observables, this mirage would fade away.
The author’s argument is simple. While the central measure of a language model’s performance is the ‘error per token’ metric (which measures how well a model can generate the next symbol in the sequence), the tasks for which we have seen emergence tend to be extremely complex, non-linear functions of this fundamental metric. Instead, if you look at functions linear in ‘error per token’, such transitions go away. For example, suppose I want the AI model to predict an answer to the Wordle game, which requires it to produce a correct sequence of five letters. If each token has a success probability of p, the accuracy at getting the exact right answer scales like $p^5$. It is also not surprising that as p increases gradually, the ability to get exact answer emerges suddenly. But, if you define your accuracy as the ‘edit distance from the perfect word’, then it scales linearly in p, and you do not see any kind of emergence here.
At the crux of this debate is the fundamental question: what metrics and observables are worth paying attention to?
It seems to me that the most interesting problems people care about (making radiological diagnosis, weather forecasts, adding numbers, generating videos from text etc.) are non-linear functions of the base error-per-token parameter. The world where you only cared about linear functions would not only be boring, but likely of very limited use. As Jason Wei notes, arithmetic is an example of problem for which exactness matters. If you ask an AI model to add 250 to 130, you would demand a correct answer of 380. You could argue that 379 is closer to 380 than, say, -2.22. But, if you simply looked at “edit distance”, is it reasonable to say that 381, 038, and -380 are all equally good?
If anything, the nonlinearities are what makes things interesting. As I heat water, its internal energy increases continuously. At a particular temperature, the water inevitably boils, with a sudden change in density (which happens to be a non-linear function of free energy). If you only looked at the internal energy, you wouldn’t even notice the water boiling. And, the “observable” phases of water and the fact that liquids tend to boil (with steam being the result of this emergence) are arguably more interesting than invisible attributes like internal energy.
This is by no means a slight on the work by Schaeffer et al. These arguments about metrics are symptomatic of a field undergoing rapid progress, and this work provides a fresh counterpoint to feverish conversations about emergence. Also, the second thrust of their work, where they show that, even for non-linear metrics, emergence fades away once you take enough data to measure accuracy is also super interesting, and I wish I understood it better. At any rate, as grandiose the term “emergence” sounds, all these works seem to be pointing at something utterly banal and boring: “nice linear things happen if you look at linear functions, and strange non-linear things happen if you look at non-linear functions.”
- January 2023